Математика в архитектуре и искусстве
Математика и архитектура
Применение теоремы Пифагора в строительстве
Многогранники, тела вращения и храмы Святого Белогорья
Математика и хореография
Симметрия в искусстве
« Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г.Вейль»
Симметрия – в переводе с греческого означает «соразмерность, пропорциональность».
Симметрия – её важнейшим свойством является сохранение тех или иных признаков по отношению к вполне определенным преобразованиям
- Картина – это отнюдь не цветная фотография. Взаимное расположение фигур, сочетание поз и жестов, выражения лиц, чередование цвета, комбинация тонов – всё это тщательно обдумывается художником, заботящемся об определенном эмоциональном воздействии картины на зрителя. Используя симметричные и асимметричные, художник должен создать нечто, обладающее в целом скрытой симметрией.
- О своей работе над картиной «Боярыня Морозова» Василий Иванович Суриков писал так: «А какое время надо, чтобы картина утряслась так, чтобы переменить ничего нельзя было. Действительные размеры каждого предмета найти нужно. Важно найти замок, чтобы все части соединить. Это – математика».

- Конечно, трудно анализировать симметрию (или как выразился художник, математику) такой сложной картины как «Боярыня Морозова». Однако можно проделать простой опыт,
обнаруживающий наличие в картине некой скрытой симметрии. Надо посмотреть на изображение этой картины в зеркале, то есть поменять в картине левое и правое (и наоборот). Оказывается, что при этом загадочный эффект движения саней исчезает.
- Можно обратиться к картине гениального итальянского художника и ученого Леонардо да Винча «Мадонна Литта».

Обратите внимание: фигуры
мадонны и младенца вписываются в правильный треугольник, который в следствии своей симметричности особенно ясно воспринимается глазом зрителя. Благодаря этому мать и ребенок сразу же оказываются на переднем плане. Голова мадонны совершенно точно, но в тоже время естественно помещается между двумя симметричными окнами, просматриваются спокойные горизонтальные линии пологих холмов и облаков. Всё это создает ощущение покоя и умиротворенности, усиливаемое за счет гармоничного сочетания голубого цвета с желтоватыми и красноватыми тонами.
Математика и музыка
Музыка была отправным пунктом в пифагорейском учении о числе. Одним из первых музыкальным инструментом древних греков был монохорд – длинный ящик для усиления звука с одной натянутой струной, которая снизу поджималась передвижной подставкой для деления струны на две отдельно звучащие части.
Как музыкальный инструмент монохорд покажется нам примитивным, но он стал прекрасным физическим прибором и учебным пособием, на котором пифагорейцы постигали премудрости музыкальную грамоту.
По преданию, сам Пифагор установил законы, на которых основывалась вся пифагорейская теория музыки:
- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна её длине l:
f=a/l,
где а – коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т.д.)
- Приятные звуку созвучия, в музыке — совершенные консонансы, получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т.е. 1:2, 2:3, 3:4.
Эти интервалы позже получили названия по латинским числительным, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава – восьмая, квинта – пятая, кварта – четвёртая (октава – 1 : 2, квинта – 2 : 3, кварта – 3 : 4).
Деление струны монохорда на части, образующие с ней совершенные консонансы
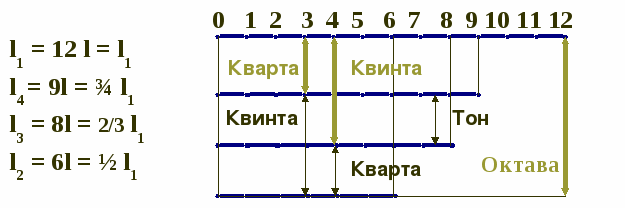
Квинта есть среднее гармоническое длин струн основного тона l1 и октавы l2
l3 =2l1l2/(l1+l2)
Октава есть произведение квинты на кварту или
l2/l3 = l4/l1
Кварта есть среднее арифметическое длин струн основного тона l1 и октавы l2
l4 = (l1+l2)/2
Построение пифагорейской музыкальной гаммы
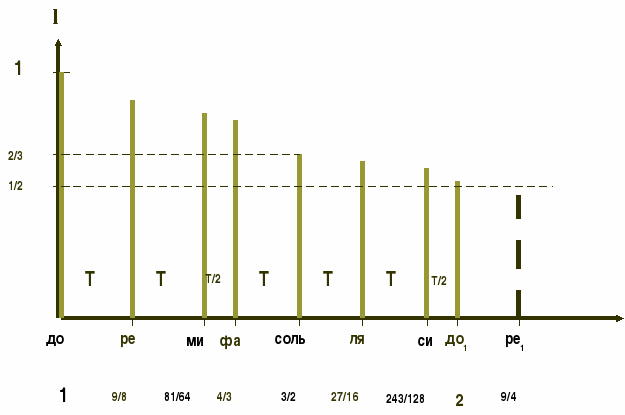
Построение музыкальной гаммы обладает такой особенностью: двигаясь по квинтам вверх и вниз, не получится точного октавного повторения исходного звука. Лишь 12 квинт приближенно равны 7 октавам, а разделяющий их интервал называется пифагоровой коммой. Несмотря на свою малость, пифагорова комма на протяжении столетий «резала ухо» музыкантам. Взяв отношение (3/2)12:27, можно найти численное значение пифагоровой коммы (1,0136).
На протяжении многих столетий музыканты настраивали инструменты так, как это делали в Древней Греции. Однако этот настрой не мог казаться им полностью подходящим, поскольку в нём сохранилась «пифагорова комма». Она была следствием несовершенства не только пифагорейской музыкальной гаммы, но и учения о числе. Теорию музыки оказалось возможным улучшить только после достаточного развития математики иррациональных величин.
Но прежде, чем в науке утвердилось новое учение о числе , прежде, чем появился новый музыкальный строй, прошла целая эпоха.
МУЗЫКАЛЬНЫЙ СТРОЙ, система отношений звуков по высоте. Тот или иной музыкальный строй характеризуется рядом чисел, каждое из которых показывает отношение частот колебаний верхних и нижних звуков интервала. Для одноголосной музыки ряда европейских народов типичен Пифагоров строй, в котором в качестве основы используется чистая квинта с отношением частот 3:2. Примерно с 16 в. в многоголосной музыке распространился т. н. чистый строй. В нем, кроме квинты, основанием служит большая терция (5:4). К началу 18 века утвердился равномерно-темперированный строй, в котором чистая октава (2:1) поделена на 12 равных полутонов ( Темперация).
Простой математический анализ многих музыкальных шедевров позволяет совершенно иными глазами взглянуть на них, увидеть их скрытую внутреннюю математическую красоту, которую мы только ощущаем, слушая произведение.
«При взгляде на математические схемы музыкальных произведений… невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества» Розенов
Хроматическая фантазия Баха
Мы находим в произведениях Баха детальную и органическую сплочённость. Закон золотого деления проявляется в них с поразительной точностью в соотношениях крупных и мелких частей, как в строгих, так и в свободных формах, что, несомненно, соответствует характеру этого гениального композитора.
Лунная соната Бетховена
В «Лунной сонате» проявление закона золотого сечения глубоко логично, оно указывает на силу темперамента Бетховена и в точности совпадает со всеми моментами высшего напряжения чувств.
Увертюра к опере «Руслан и Людмила» Глинки
Простейший математический анализ музыкальных произведений М.И. Глинки убеждает в применении закона золотого сечения только лишь в широких масштабах при полном отсутствии мелочных соответствий.
Итак, гармония космоса была воплощена пифагорейцами в сфере музыки. Идея совершенства окружающего мира владела умами ученых и в последующие эпохи. В первой половине XVII в. И.Кеплер установил семь основных гармонических интервалов: октаву — 2/1, большую сексту — 5/3, малую сексту — 8/5, чистую квинту — 3/2, чистую кварту — 4/3, большую терцию — 5/4 и малую терцию — 6/5. С помощью этих интервалов он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармоничных отношений «на небе», проделав огромную вычислительную работу, И.Кеплер установил, что отношения экстремальных углов скоростей для некоторых планет близки к гармоническим: Марс — 3/2, Юпитер — 6/5, Сатурн — 5/4.
До сих пор никому не удавалось найти алгоритм, порождающий простую и красивую мелодию. Мы просто не знаем, какое волшебство происходит в голове композитора, создающего неповторимую мелодию. Гениальное произведение — это результат вдохновения и мастерства его создателя. А еще своеобразная тайна, постичь которую порой невозможно. Решая задачи и слушая великую музыку, мы открываем в ней совершенство, простоту, гармонию и еще нечто такое, что неподвластно выражению словом…
Список литературы
Асмус А.Ф. «Античная философия». М.:Высшая школа-76, 543.
«Атеистический словарь» (под ред. М.П. Новикова). М.: Политиздат-83, 559.
«Аум»-N2 (альм. «Русского эзотерического общества Нью-Йорка, под ред. П. Рогальской и др.). Терра-90, 322.
А.В. Волошинов «Математика и искусство».М.: Просвещение – 92, 336
«Философский словарь» (под ред. И.Т.Фролова). М.:из-во полит.лит-ры-87, 588.
Вл.Чешак и др. «История философии в кратком изложении»(пер. с чешского — И.И.Богута). М.:Мысль-91, 592.
Э.Шюре «Великие посвящённые» (пер. с франц. Е.Писаревой).Репринт издания 1914, 419.
А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год
А.В. Волошинов «Математика и искусство», Москва, «Просвещение», 1992 ГОД
Энциклопедический словарь юного математика Москва 1989 год.
И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.
DVD Tsarskoe selo Master Video, 2004
CD Microsoft Office at school
